Programación de GPU en Haskell usando GPipe - Parte 2
Nota: estas leyendo la traducción al castellano de una serie de tutoriales en ingles sobre GPipe; la versión original, escrita por Tobias Bexelius (creador de GPipe), se encuentra aqui.
< Episodio previo: Hello triangle
¡Bienvenido nuevamente! En la ultima parte obtuviste tu primer triangulo mediante GPipe. Esta vez vamos a examinar Buffer y PrimitiveArray con más detalle.
Buffers
En el ejemplo "Hello world" que hicimos la ultima vez, usamos un Buffer para almacenar las posiciones y colores del triangulo. A partir de este buffer, creamos un PrimitiveArray que enviamos al shader. Más adelante vamos a ver que un Buffer puede ser usado también para otras cosas.
Un Buffer en GPipe es un array de datos que esta almacenado en la GPU. Es mutable, así como IOArray o STArray, y así como aquellos también vive en una monada, en este caso la monada ContextT. Veamos primero la función que se encarga de crear buffers:
newBuffer :: (MonadIO m, BufferFormat b) => Int -> ContextT w os f m (Buffer os b)
Un buffer tiene tipo Buffer os b, donde os es el mismo que el de ContextT. Como puedes recordar desde la ultima vez, este parámetro de tipo os es usado para evitar que los objetos asociados a un contexto puedan escapar de la monada, y Buffer es uno de esos objetos.
newBuffer solo toma un argumento: el numero de elementos a crear en el buffer. Un buffer tiene elementos mutables, pero el numero de elementos es inmutable. El tipo de los elementos del buffer se denota con b, y puedes ver que este b esta delimitado por el typeclass BufferFormat b. Antes de mostrarte ese typeclass, miremos la función que vas a usar para llenar el buffer con datos desde el lado de la CPU:
writeBuffer :: MonadIO m => Buffer os b -> BufferStartPos -> [HostFormat b] -> ContextT w os f m ()
Esta función toma un buffer para escribir y una posición de inicio con indice basado en cero, nada extraño en esto, pero luego toma una lista de HostFormat b... ¿Que ocurre con esto? Los contenidos de un buffer no tienen la misma representación en el host que en el buffer, el cual vive en la GPU (desde ahora voy a usar el termino host cuando me refiero al entorno normal de Haskell que vive en la CPU, en contraposición al mundo de la GPU). HostFormat b es un tipo al typeclass BufferFormat b. Miremos ese typeclass:
class BufferFormat f where
type HostFormat f
toBuffer :: ToBuffer (HostFormat f) f
El único propósito de esta clase, es proveer una representación para el tipo de los elementos del buffer en el host, así como una conversión de la representación del host a la del buffer. Aquí hay algunos ejemplos de instancias de esta clase, y sus representaciones en el host:
| f | HostFormat f |
|---|---|
| B Float | Float |
| B Int32 | Int32 |
| B Word32 | Word32 |
| B2 Float | V2 Float |
| B2 Int32 | V2 Int32 |
| B2 Word32 | V2 Word32 |
| B2 Int16 | V2 Int16 |
| B2 Word16 | V2 Word16 |
| (a, b) | (HostFormat a, HostFormat b) |
| V2 a | V2 (HostFormat a) |
Hay muchas más instancias, incluyendo B3, B4 y tuplas mas grandes. Mira la lista completa en hackage.
Un Float en el host se convertirá B Float en el Buffer. B a es un tipo opaco de cual no puedes inspeccionar su valor o hacer ningún calculo, por ej. no hay instancia de Num para B Float. Para Buffer no se expone una manera de aplicar funciones en sus elementos de ninguna manera (por ej. Buffer no posee instancia del typeclass Functor), pero vamos a crear pronto un VertexArray a partir de nuestro Buffer y entonces será distinto.
GPipe también define los tipos B2 a, B3 a y B4 a. Para un conjunto selecto de a, B2 a es la representación en el buffer de un V2 a en el host. V2 a es también una instancia de BufferFormat con V2 (HostFormat a) como representación en el host, lo cual significa que tanto V2 (B Float) como B2 Float tienen la misma representación en el host: V2 Float. Ambos formatos de buffer tienen el mismo tamaño e incluso disposición interna, pero B2 Float puede ser usado de manera más eficiente como vamos a ver luego. Por esta razón, siempre intenta usar tipos B en vez de tipos V en los buffers, cuando sea posible. Entonces, ¿porque hay una instancia de BufferFormat para V2? El caso de uso principal es el de las matrices, por ej. V4 (V4 Float) en el host puede almacenarse en un buffer como V4 (B4 Float).
Otra cosa interesante que puedes haber notado al estudiar la lista de instancias de BufferFormat, es que hay instancias de B2 Int16 y B2 Word16, pero no de B Int16 ni B Word16. Esto es porque los atributos de los vértices tienen que estar alineados a 4 bytes en algunas piezas de hardware, y GPipe respeta esto en sus tipos de datos. Int16 y Word16 son ambos de 2 bytes, así que necesitas tener un vector de al menos dos de ellos. Hay instancias de B3 Int16 y B3 Word16, pero estas poseen un relleno (padding) de 2 bytes extra. La motivación para esto es que siempre podrías usar B Int32 en vez de B Int16 si existiese, funcionarían con los mismos shaders y serian del mismo tamaño de todas formas si agregamos el relleno para el segundo. Por otra parte, un B3 Int32 toma 12 bytes mientras que un B3 Int16 con relleno incluido solo ocupa 8 bytes, así que hay un caso distintivo para este ultimo. Un B4 Int16 también utiliza 8 bytes, pero no funcionaria con los mismos shaders, como va a ser evidente en la siguiente parte de este tutorial.
Ahora miremos el miembro toBuffer del typeclass BufferFormat. Posee el tipo ToBuffer (HostFormat f) f. ToBuffer es algo llamado arrow en Haskell. Es como una función (en este caso HostFormat f -> f), pero más general. Echemos un vistazo a la instancia BufferFormat (a, b) como ejemplo:
{-# LANGUAGE Arrows #-}
instance (BufferFormat a, BufferFormat b) => BufferFormat (a, b) where
type HostFormat (a,b) = (HostFormat a, HostFormat b)
toBuffer = proc ~(a, b) -> do
a' <- toBuffer -< a
b' <- toBuffer -< b
returnA -< (a', b')
La notación arrow casi se parece a un lambda (usando el keyword especial proc) retornando una acción monadica. Pero no es una monada. La mayor diferencia con una monada es que no puede seleccionar una acción basándose en los valores de retorno del arrow. Es por esto que las acciones de un arrow poseen una cola (-<); cualquier cosa entre las partes <- y -< de un arrow, no puede referenciar nada fuera de ellas (a, b, a', b' en este caso). Esto obliga a que toda invocación a toBuffer deba ir a través de la misma serie de acciones de arrow, independientemente de los valores de entrada reales. Otro requerimiento adicional que tiene GPipe, es que necesita ser capaz de producir valores de forma lazy, es por ello el tilde (~) en el patrón proc. Las únicas acciones del arrow ToBuffer que GPipe define para usar en tu propia implementación de toBuffer, son los métodos toBuffer de otras instancias. Vas a ver aparecer este patrón, donde un arrow es usado para definir la conversión entre dos dominios, en varios lugares de GPipe a medida continuemos con el tutorial.
Arrays de vértices
Bueno, ¡ahora eres un experto en buffers! Vamos a darles algún uso:
newVertexArray :: Buffer os a -> Render os f (VertexArray t a)
Ejecutas esta función en una monada Render para crear un VertexArray t a. Un array de vértices es como la vista de un buffer, y newVertexArray no copia ningún dato. Ya que operamos dentro de la monada Render (que es ejecutada por la función render, la cual no permite valores de retorno), y un Buffer solo puede ser modificado fuera de esta monada (en la monada ContextT), conceptualmente podrías pensar a VertexArray como una copia del Buffer. No lo es realmente, pero puedes tratarlo como una.
VertexArray t a es un array de vértices donde cada vértice es un elemento de tipo a, que es el mismo tipo de los elementos del Buffer a partir del cual lo creaste. No te preocupes por el parámetro T por ahora, vamos a llegar a eso en un momento. El VertexArray posee tantos vértices como elementos pertenecientes al Buffer que lo origina, pero en contraste a este ultimo, puedes recortar un VertexArray usando las funciones dropVertices o takeVertices. Estas funcionan exactamente como drop o take trabajan sobre listas normales:
takeVertices :: Int -> VertexArray t a -> VertexArray t a Source
dropVertices :: Int -> VertexArray () a -> VertexArray t a Source
VertexArray también tiene una instancia de Functor, la cual permite aplicar fmap sobre los vértices. ¡Aqui es donde la opacidad de los tipos B entran en juego! Ahora que puedes hacer cosas con tus valores B, vas a notar que las opciones son algo limitadas. Puedes simplemente agarrar elementos de estructuras como tuplas y/o construir nuevas estructuras con los valores que posees. A pesar de esto, hay un par de funciones que operan sobre valores B que puedes usar aquí:
toB22 :: forall a. (Storable a, BufferFormat (B2 a)) => B4 a -> (B2 a, B2 a)
toB3 :: forall a. (Storable a, BufferFormat (B3 a)) => B4 a -> B3 a
toB21 :: forall a. (Storable a, BufferFormat (B a)) => B3 a -> (B2 a, B a)
toB12 :: forall a. (Storable a, BufferFormat (B a)) => B3 a -> (B a, B2 a)
toB11 :: forall a. (Storable a, BufferFormat (B a)) => B2 a -> (B a, B a)
Estas permiten separar vectores B en partes mas pequeñas. Fijate que de todos modos no hay funciones que puedan combinarlas nuevamente.
Puedes también hacer comprimir (zip) dos VertexArray juntos, con la función zipVertices, que funciona exactamente como zipWith para listas normales; provees una función para combinar los elementos de ambos argumentos VertexArray y el resultante sera del tamaño del más pequeño de ambos arrays:
zipVertices :: (a -> b -> c) -> VertexArray t a -> VertexArray t' b -> VertexArray (Combine t t') c
(Nuevamente, no te preocupes por el extraño primer parámetro en el VertexArray retornado, lo explicaré más adelante)
Comprimir arrays de vértices es lo que se corresponde con usar arrays no-intercalados (non-interleaved) en OpenGL, mientras que un array de vértices desde un solo buffer de un tipo de elementos compuestos (así como una tupla de dos valores B) corresponde a arrays intercalados (interleaved). ¡Esta es solo la manera funcional y type safe de hacerlo!
Arrays de primitivas
Ahora que haz recortado (trim), comprimido (zip) y mapeado (fmap) tus arrays de vértices a la perfección, es hora de crear un array de primitivas. La manera más simple de crear uno es con esta función:
toPrimitiveArray :: PrimitiveTopology p -> VertexArray () a -> PrimitiveArray p a
Siempre vas a necesitar una topología de primitivas, ademas de tu array de vértices, para crear un PrimitiveArray. La topología de primitivas denota como los vértices deben conectarse para formar primitivas, y es uno de estos constructores:
data PrimitiveTopology p where
TriangleList :: PrimitiveTopology Triangles
TriangleStrip :: PrimitiveTopology Triangles
TriangleFan :: PrimitiveTopology Triangles
LineList :: PrimitiveTopology Lines
LineStrip :: PrimitiveTopology Lines
LineLoop :: PrimitiveTopology Lines
PointList :: PrimitiveTopology Points
En la mayoría de los casos vas a trabajar con triángulos. Veamos como se ven las tres topologias de triángulos:
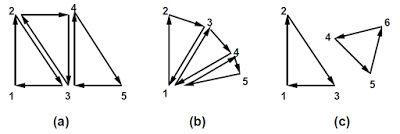
En un TriangleStrip, cada vértice forma un triangulo con los dos vértices previos, alternando el camino de los vértices para cada triangulo. Esto significa que el primer triangulo es formado por los vértices 1-2-3 en ese orden, el siguiente por 2-4-3, luego por 3-4-5, 4-6-5, y así sucesivamente. Para TriangleFan, cada triangulo es formado por el primer vértice en el array junto con cada dos vértices consecutivos, en ese orden. Para TriangleList, cada tres vértices simplemente forman un triangulo; no se comparte ningún vértice entre los triángulos.
Los vértices siempre vienen en orden antihorario para un triangulo de cara orientada hacia el frente (lo cual significa que todos los triángulos en la imagen de arriba, excepto el de más a la derecha, están orientados con cara hacia el fondo; solo como ejemplo de cuan intuitiva puede ser la especificación de OpenGL). La orientación de la cara de un triangulo va a ser importante luego, cuando lo rastericemos, en ese momento podrás elegir solo rasterizar los triángulos de cara hacia el frente o hacia el fondo.
Los arrays de primitivas no se pueden recortar como los de vértices, pero poseen una instancia de Functor así que puedes hacer fmap sobre ellos exactamente como con los arrays de vértices. También tienen una instancia de Monoid, que permite concatenar dos PrimitiveArray juntos en uno solo usando mappend. Esto hace posible crea un PrimitiveArray conformado por varias tiras de triángulos disjuntas, pero maneras más eficientes de lograrlo serán presentadas en las siguientes dos secciones.
Arrays de indices
Es común que un vértice sea usado no solo por dos triángulos consecutivos en una tira, sino también por triángulos de otra tira. Seria un desperdicio duplicar para cada tira todos los datos de los vértices compartidos, y por esta razón puedes usar un index array como reemplazo:
toPrimitiveArrayIndexed :: PrimitiveTopology p -> IndexArray -> VertexArray () a -> PrimitiveArray p a
En vez de formas primitivas tomando vértices consecutivos en un VertexArray, esta función va a tomar los indices de un IndexArray y usarlos para referenciar vértices del VertexArray. Múltiples elementos en el IndexArray pueden referirse al mismo vértice. La topología de primitivas funciona de la misma manera para esta función, pero es aplicada al IndexArray. Por ejemplo, si TriangleStrip es usado, el primer triangulo es formado por los vértices referenciados por los primeros tres indices, el siguiente esta formado por el segundo, el cuarto y el tercer indice, y así sucesivamente.
Puedes crear un IndexArray usando
newIndexArray :: forall os f b a. (BufferFormat b, Integral a, IndexFormat b ~ a) => Buffer os b -> Maybe a -> Render os f IndexArray
Muy parecido a crear un VertexArray, pero el tipo de los elementos del Buffer a partir del cual lo creas, esta también acotado por el siguiente type family:
type family IndexFormat a where
IndexFormat (B Word32) = Word32
IndexFormat (BPacked Word16) = Word16
IndexFormat (BPacked Word8) = Word8
Esto significa que los indices pueden ser Word32, Word16 o Word8. ¿Recuerdas que previamente mencioné que todos los tipos de los elementos del buffer necesitaban tener una alineación de 4-bytes? Los arrays de indices realmente requieren que todos los elementos estén empaquetados, pero todavía soporta indices de tipo Word16 y Word8. Esto significa que los buffers de estos dos tipos de elementos no pueden ser usados como arrays de vértices. Esto es por lo que la representación de Word16 y Word8 es BPacked Word16 y BPacked Word8. Estos funcionan exactamente como sus contrapartes B, con la excepción de que no hay instancias de VertexInput para ningun BPacked a. VertexInput es el type class usado en la creación de streams de primitivas desde arrays de primitivas, lo cual vamos a usar en la siguiente parte de este tutorial. Como puedes suponer a esta altura, el type family IndexFormat a evalúa a los mismos tipos que el tipo asociado HostFormat a.
Además de un buffer de indices, newIndexArray también toma un Maybe a como argumento. Esto denota un indice opcional llamado primitive restart, es decir un valor de indice especial, que si es encontrado en el array de indices mientras se procesan las primitivas, señala que la topología actual debe terminar y el siguiente indice es el comienzo de una nueva topología. Esto hace posible tener múltiples tiras de triángulos en un solo IndexArray con solo separarlos con un indice especial, lo cual es mucho más eficiente que concatenar múltiples PrimitiveStream usando su instancia de Monoid.
Los arrays de indices pueden ser recortados como cualquier array de vértices, pero siempre usando las funciones takeIndices y dropIndices. No poseen instancia de Functor (lo cual no tiene sentido) ni de Monoid.
Arrays de primitivas instanciados
La ultima cosa que voy a mostrarte en este episodio son los arrays de primitivas instanciados. Imagina que quieres crear una malla de triángulos de un templo, donde tienes muchos pilares idénticos ubicado en fila. En vez de duplicar los triángulos de cada pilar, o hacer un solo array de primitivas para concatenarlo consigo mismo múltiples veces, puedes crear un array de primitivas instanciado. La función de ve así:
toPrimitiveArrayInstanced :: PrimitiveTopology p -> (a -> b -> c) -> VertexArray () a -> VertexArray t b -> PrimitiveArray p c
Es muy similar a la función zipVertices en que toma dos VertexArray y una función binaria para combinar los vértices de estos arrays, pero toPrimitiveArrayInstanced no junta los dos arrays. En cambio, va a crear un array de primitivas desde el primer array de vértices para cada vértice del segundo array, y concatenar los resultados. En nuestro ejemplo de los pilares del templo, el primer array contiene entonces la tira para un solo pilar, mientras que el segundo array contiene una posición para instanciar cada pilar, resultado en un array de primitivas donde cada vértice contiene su posición individual dentro del pilar, asi como la posición de la instancia dentro del templo. Necesitarias entonces un shader que combine estas dos posiciones juntas en la posición final. Esta es la manera más eficiente de renderizar múltiples instancias de un mismo objeto.
Si quieres usar un arrays de primitivas instanciados y array de primitivas indexados al mismo tiempo, hay una función para hacer eso también:
toPrimitiveArrayIndexedInstanced :: PrimitiveTopology p -> IndexArray -> (a -> b -> c) -> VertexArray () a -> VertexArray t b -> PrimitiveArray p c
Para hacer la instanciación aun más poderosa, puedes replicar los vértices en un array un numero fijo de veces cada uno y luego comprimirlo con otro array y usar el resultado como instancias en toPrimitiveArrayInstanced. Por ejemplo, podrías tener un array de vértices con tres diferentes colores, replicar cada color 5 veces, luego comprimirlo con un array de 15 posiciones, y usar esto como instancias de nuestro templo para tener 15 pilares de colores en tres diferentes graduaciones para variar. La función que usarías para hacer esto es:
replicateEach :: Int -> VertexArray t a -> VertexArray Instances a
Esto va a replicar cada vértice en el array de argumento tantas veces como sea dictado por el primer argumento. Fijate que el tipo de Instances en el primer parámetro de tipo del resultante VertexArray. Quizás hayas notado que este parámetro había sido previamente () o solamente t. Si este parámetro de VertexArray es Instances entonces el VertexArray solo puede ser usado para instancias, es decir como ultimo argumento en una llamada a toPrimitiveArrayInstanced o toPrimitiveArrayIndexedInstanced. Si vas hacia atrás y miras los tipos de las funciones que toman o retornan VertexArray más arriba, vas a notar que:
replicateEachretorna unVertexArrayque debe ser usado como instancia.dropVerticesno puede ser usado en ningúnVertexArrayque deba ser usado como instancia.zipVerticesretorna unVertexArrayque debe ser usado como instancia si alguno de los arrays de entrada debe ser usado como instancia.
Fui un poco injusto ahora, porque esto ultimo no era algo que pudieses notar solo mirando el tipo de la la función, necesitabas esta definición también:
type family Combine t t' where
Combine () Instances = Instances
Combine Instances () = Instances
Combine Instances Instances = Instances
Combine () () = ()
Cuando tienes tu PrimitiveArray, la información de tipo ya sea si fue instanciado, indexado o ambos, se ha ido. Esto significa que puedes usar mappend sobre un array de primitivas instanciado junto con uno no instanciado, y que el shader al cual envías un array de primitivas no le importa si era instanciado o indexado.
Esta vez no hay ejemplos de código, así que voy a dejar como ejercicio aplicar lo que aprendiste esta vez en el ejemplo de la parte anterior. La próxima vez finalmente vamos a abordar Shader!